WSU Engineering Statistics 360
Class notes from session 8. October 20, 2000.

There are no new notes for this class session. Please refer to the notes from last year, below, for additional information.

The usual list of observations and comments

We survived the mid-term exam on Friday October 8, but just barely. Here are observations that I made regarding the exam and progress in the class in general.

• A number of people have been producing diagrams with Excel that they have labelled "histograms," but which are not histograms. They are bar graphs. It wasn't until I observed one student producing these in real-time that I finally figured out what is up. A histogram is a bar-graph, but it is one in which the data have been sorted into "bins." The histogram simply plots the frequency with which data fall into each bin against the center value of the bin. If you examine my sample Excel spreadsheet you'll find a histogram produced with the data analysis add in for Excel. If the "Tools" menu in your copy of excel does not have a "Data Analysis" option, then you must run the add in to prepare it. Run the histogram option of the data analysis package, and provide the list of data values and the bins.
• My cursory examination of the test results show that a few people in the class understand everything quite well. The vast majority of the class are somewhat vague, though. You in this last category are poking all around the correct methods and analysis, but not quite putting it all together. I am going to try to explain the remaining unclear things and maybe this will be enough to push most people past the barriers. Thus, on Friday October 15, I roll up my sleeves and redouble all previous efforts.
• We need to work more homework problems. Only practice makes a person proficient with this material. I have been away from it for a decade and all of you can see that I'm a tad rusty. Thus, we will work more problems in class and at home. It would help a lot if the class actually allowed 3 hours of class time, and met twice a week. There's nothing we can do about this at the present time.
• Also on Friday, October 15, we must discuss projects. I have been meaning to do this for two weeks, but other things always distract me. Everyone remind me in class--discuss projects.
• Check out answers to the exam on the bulletin board across from my office on the first floor of the classroom building.
• The final exam will be atake home exam of slightly greater length.

Special Topic: Bayesian Estimation Part I.

In a recent treatise on inference one statistician/physicist claimed there is "...a good excuse for not using Bayesian methods, that being incompetence." Our textbook refers to Bayes only through its listing of Bayes Rule on page 74. Nowhere does it indicate any use for Bayes rule, however. I'll attempt to explain Bayesian methods by way of example in these notes. I think you'll be able to see why it has certain appeal.

Bayesian estimation begins with Bayes theorem.

P(X|Y)=P(Y|X)P(X)/[P(~X)P(Y|~X)+P(X)P(Y|X)]
where ~X means not X.

We interpret this as, the probability of event X, given the information that Y has occured is equal to the probability of event Y given that X has occurred times the probability that Y occurs itself, divided by the total probability of Y occuring. The denominator in Bayes Rule is known as the Total Probability. It is a normalizing factor and often people utilize Bayes Rule by ignoring it. What Bayes Rule provides is a template for modifying our biases (a priori beliefs) concerning the probability of event Y based on data that we observe. We can even make the modifications in real time. Let's consider an example that involves discrete probability.

Suppose we are driving west on I-80 in central Nebraska knowing that there is a snow storm ahead of us either in Wyoming or Colorado. The cars coming toward us have come either from Colorado on I-76 or from Wyoming on I-80. We assume that the numbers of cars coming from either highway are the same. Some of the cars coming from Colorado will have Wyoming plates, and some coming from Wyoming will have Colorado plates. We think that the cars coming from I-80 are equally divided between Wyoming and Colorado plates. Those coming from Colorado are 4 times as likely to have Colorado plates as Wyoming plates. What we wish to do is observe cars coming toward us covered with ice and snow and decide where it is storming.

If we consider only the next two snow covered cars, then the entire universe of possibilities we can summarize on an event tree like that below, with the given probabilities of traveling down each branch of the tree.

Where it snows         Plate on Car 1       Plate on Car 2

Colorado ------------>  Colorado (0.8) -------> Colorado (0.8)
                 |                         |
                 |                          --> Wyoming (0.2)
                 |
                 ---->  Wyoming (0.2) --------> Colorado (0.8)
                                           |
                                            --> Wyoming (0.2)

Wyoming  ------------>  Colorado (0.5) -------> Colorado (0.5)
                 |                         |
                 |                          --> Wyoming (0.5)
                 |
                 ---->  Wyoming (0.5) --------> Colorado (0.5)
                                           |
                                            --> Wyoming (0.5)

Since we have no information about where it is snowing ahead, we make the a priori assumption that it is equally likely to be snowing in Wyoming or Colorado (each have probability 0.5 for instance). Suppose that the next two snowy cars have Wyoming plates. How can we use this information to modify the probability of snow in either state? Well, I suppose we should use Bayes Rule.

From our a priori assumptions...

P(Snowing in Wyoming)=P(W)=0.5
P(Snowing in Colorado)=P(C)=0.5

And from the event tree...

Probability that we observe two Wyoming cars if they have come from  
Wyoming=P(Wy,Wy|W)=0.25

Probability that we observe two Wyoming cars if they have come from
Colorado=P(Wy,Wy|C)=0.04

P(W|Wy,Wy)= 0.5*0.25/[0.5*0.25+0.5*0.04] = 0.862
Likewise
P(C|Wy,Wy)= 0.5*0.04/[0.5*0.25+0.5*0.04] = 0.138
Which add to a probability of 1.0 as we should expect.

Therefore the observation of two icy cars with Wyoming plates has increased the probability that it is snowing in Wyoming to 0.862 and decreased the probability that it is snowing in Colorado to 0.138. We can now use these posteriori probabilities as new prior probabilities while we observe more snow covered cars, and continually update our expectations. Hopefully, before we get to the I-76/I-80 junction we will know whether to turn north or south.

Special Topic: Bayesian Estimation Part II.

To use Bayes Rule for parameter estimation in the case of a continuous probability distribution I make the following modifications. First, I ignore the total probability denominator. It is utterly immaterial to our results. Let Y now stand for observed data and other information, and let X stand for the parameter values of our model. Then we interpret Bayes Rule as follows.

The probability of certain values for model parameters, given the data I have observed and whatever else I know about the situation, equals the probability of having observed these particular data given that these specific parameter values are true, times what I believe to be the probability of these parameter values being true before I have observed any data. That is horribly complicated, I know, but read it several times while following through the terms in the formula. If it still isn't clear, don't dwell on it. Go have a beer with your friends.

P(parameters|data,information)=P(data|parameters)P(parameters,information)

The troublesome part of this formula is what to use for P(data|parameters). This is some kind of function that drives us toward good estimates of the parameter values. Without any justification other than "it seems like a good idea" I'll equate the term P(data|parameters) with a likelihood function. You'll recall that the likelihood function gave very reasonable estimations in earlier examples, so it seems reasonable to use it here as well. There are other ideas concerning this, but I won't go into them now.

Many people think the troublesome part of this recipe is the prior probability, P(parameters,information), because they see this as being subjective, and adding nothing but prejudice to the final result. However, this is not so. The following example ought to demonstrate that the prior probability is important only when our data are very poor (i.e. contain little information regarding parameters) or very limited in number.

In this first example I will use 8 observed values of time to failure to estimate the failure rate. You may recall that in the case of a constant rate of failure the exponential probability distribution applied, and that the likelihood function in this case is...

L(l)=l8e-l(a+...+h)
where a,...,h are the 8 observed times to failure.

Rather than use the product likelihood function above, I suggest using P(y)=l e^-yl alone as the likelihood function, and simply applying it iteratively. That is I apply it with the first data point using the prior, and use the posterior probability as the prior for the next data point, and so forth. As for a prior probability; well, I know absolutely nothing about the problem so I may as well assign a constant probability of 1.0 to all possible values of l.

The data values are 2.40, 2.50, 2.38, 2.63, 2.78, 2.65, 2.68 and 2.69; which average to a failure rate of 0.40 per unit time. The diagram below shows the posterior probability after 1, 4, and 8 data values have been applied through the likelihood function. What you notice is that successive applications of the recipe produce a posterior probability that is increasingly concentrated near 0.40

The next example shows both how one would apply prior information to the recipe, and also that the choice of prior is not necessarily all that important. I have used the same data as in the previous example, and added the following data values as well 2.59, 2.58, 2.60 and 2.60. Suppose that instead of having no prior knowledge about the value of l, I possessed information that suggested the value of l was twice as likely to be found in the interval 0.5 to 1.0 as it was in the interval below 0.5. The prior thus jumps up by a factor of two at a value of l = 0.5. After applying the first observation through the likelihood function, I find a posterior probability with most probabilities above 0.5 rapidly diminishing, only those near 0.5 retain their prior value, and a bit of the probability below 0.5 increased somewhat. After repeated application of data the posterior probability finally shows a peak value near 0.4 and a sharp, but diminishing peak near 0.5. If a statistician had any prejudice about l being more likely above 0.5 in value, data such as this would eventually convince him otherwise.

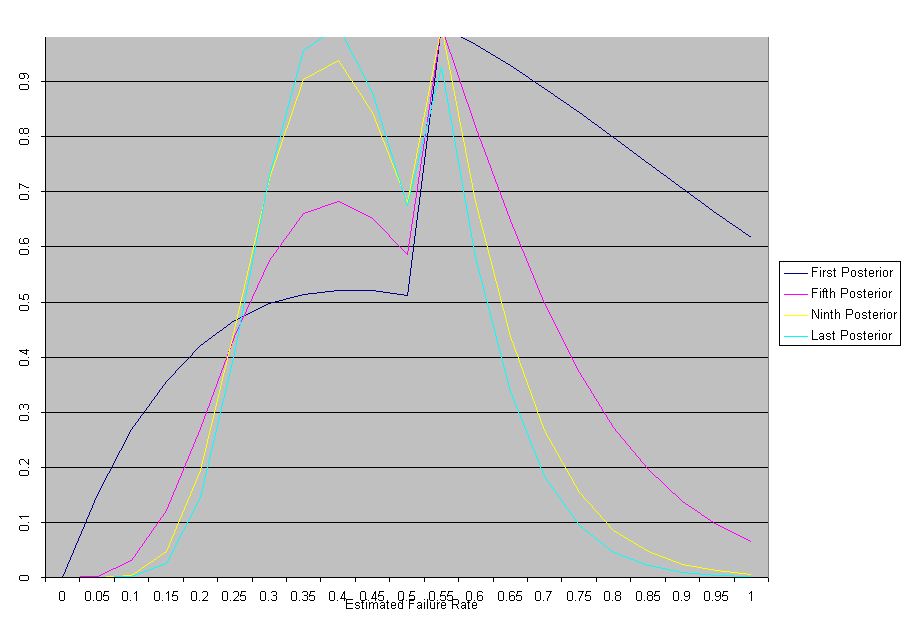
Eventually, enough high quality data can overcome a stupidly chosen prior. However, it is important to recognize that even the finest data cannot overcome a prior so stupid that it assigns a value of zero to the true parameter value.

Link forward to the next set of class notes for Friday, October 27, 2000