Stability

This page is utterly incomplete. I'm working on it.
A tornado vortex is simply a structure built of fluid. How does it remain stable and resist being dissipated immediately? The animation loop that began this web page shows a tornado vortex that is perturbed at its base and propagates disturbances as waves along its axis. The disturbance propagates along the tornado, but the tornado returns basically to its previous form. In this sense it is a stable feature. Many people have observed tornadoes with bulges or constrictions that propagate up them.
The air flow in which it is embedded carries a tornado funnel with it and draws it into all sorts of wild shapes sometimes -- shapes like arches and lariats. Yet, the vortex persists.
Even though there is no mechanism that can make a Rankine vortex in the atmosphere, it makes a simple model with which to analyze stability.
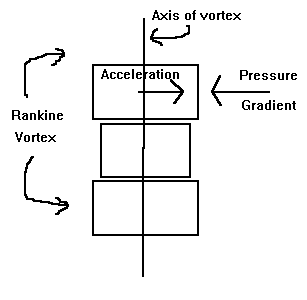
Stability comes from restoring forces that return a vortex to its original form no matter how it is deformed. The graphic below shows how the rankine vortex supplies these forces. The two forces in question are...
- A pressure gradient that pushes toward the axis of the vortex. High pressure on the outside and low pressure inside.
- A centrifugal acceleration that pushes back against the pressure gradient.
When these two forces are in balance air simply orbits around the vortex axis without there being any effective means of accelerating this rotation. That is, the Rankine vortex just spins like a solid body. The graphic shows three segments of the vortex. The larger segments are at the equilibrium size of the vortex. Suppose that the pressure inside the vortex drops slightly and the middle segment attempts to shrink as a result. Because air cannot flow into the vortex from the outside without first increasing the spin of the vortex, air above and below this segment within the vortex will flow into it to expand the segment back to equilibrium. The opposite occurs if pressure inside the vortex tries to expand it beyond equilibrium. Now, assume that the middle segment manages to shrink by some other means. In order to maintain its circulation, the smaller segment will have to spin faster. The centrifugal acceleration either exceeds the pressure force, which forces the segment to expand again, or the central pressure will have to decrease, which will draw air from above and below to expand it again. The vortex may send disturbances up and down its length, but it maintains its shape and size well.
Evolution
Even though a vortex is rather stable, the tornado evolves in a typical way as it intensifies and then dies. According to Robert P. Davis-Jones the typical life evolution of a tornado is as follows.
- First there is a dust whirl stage. There is a short funnel pendant at the cloud base and a visible dust storm at the surface. The photograph at right by Wm T. Hark shows this stage. Any damage that occurs at this stage is light.

- Next there is an organizing stage wherein the funnel cloud descends toward the ground, and wind speed increases in the dust whirl. This stage may last for a very long time, an hour perhaps, as it did in the Spencer, South Dakota tornado, or a very short time as it did in Cheyenne in 1979.
- Finally the tornado reaches a mature state where its intensity is as great as conditions will allow (anywhere from F0 to F5 intensity). The visible funnel is vertical at this time and has attained its greatest width. The accompanying photo by Wm. T. Hark shows a mature tornado at Perth, Kansas. This particular form the stormchasers call a "wedge tornado."

- As the mature stage continues the visible funnel will begin to tilt. The foot of the storm tends to lag behind its connection at cloud base. The funnel is also shrinking in width. However, damage can still be quite severe.
- The tornado continues to be stretched out into a long, thin vortex (roping out), and may even sustain sections of its length where it vanishes. It now dissipates.
A few very intense tornadoes decay quite abruptly by spreading out and becoming diffuse. It is possible in these cases that conditions of ambient rotation and suction in an updraft make a sustained, stable vortex impossible. For instance, if the updraft is very strong, and ambient rotation is weak, the inflowing air may attain enough momentum that it will flow beyond the equilibrium size of the rankine vortex. Now the surface pressure may be so low that it decelerates the updraft and brings the whole process to a halt. Then again, in this same situation, the vortex may become so small that eddy viscosity causes it to diffuse rapidly, or perhaps the eddies may assume a form that, instead of transfering momentum into the core of the vortex (Starr's hypothesis) they transfer it out.
The tornado also has a progression of typical forms that it assumes as it becomes increasingly intense. Much of this evolution is suggested by laboratory experiments and computer simulations, not all of it has been observed directly on real tornadoes. The following list explains the evolution. I compiled it from Neil B. Ward's summary of laboratory experiments (J. Atmos. Sci. 29, 1194-1204, 1972) and J.T. Snow's compilation of computer simulations (Rev. Geophy. and Space Phys. 20, 953-964, 1982). It is organized in terms of increasing maximum intensity in the mature state.
- If there is no ambient vorticity to begin with, then an updraft just draws surface air toward its center where the air ascends into the cloud. The air flow resembles that into a corner and up a wall. No vortex of any type forms.
- If there is only a small ratio of ambient vorticity to updraft (swirl ratio), then no concentrated core will form and air simply spins and rises over a broad region. Since air on the axis of this whirl has flowed into the updraft near the ground surface (i.e. corner flow once again) it will have lost most of its circulation around the updraft through friction with the ground.
- As the amount of ambient swirl increases not all of the air flowing into the updraft looses its circulation to friction. Somewhere aloft, probably well within the parent cloud, this air achieves cyclostrophic balance. At this height the spinning air is nearly a rankine vortex. The flow of air resembles an hour-glass with a wide inflow and updraft near the surface a rankine vortex at mid level and a wide divergent updraft above. The accompanying photo (below) shows such a thunderstorm in south-central Wyoming in July, 1999. I've superimposed a few arrows to suggest the airflow which the small cumulus clouds reveal.

- Increasing the swirl ratio leads to a dynamic pipe that grows upward and downward from mid levels. Near the surface the vortex can be closed-off to prevent inflowing air from destroying it. The visible vortex is smooth and laminar in this portion. Aloft, however, there is no such rigid boundary and the vortex will probably develop a central downdraft. At this time the vortex is single-celled in its lower portion, probably below the cloud base, and two-celled (Sullivan vortex) above. Atmospheric scientists refer to the boundary between the two as vortex breakdown.
- Increase the swirl ratio farther and the point of vortex breakdown descends toward the ground surface. Eventually, with enough swirl, the vortex is two-celled over its entire length. The tornado now has a downdraft at its core all the way to the ground surface. The boundary between the central downdraft and the updraft surrounding it is very turbulent. The visible vortex takes on a boiling appearance.
- Increasing the swirl still farther and the central downdraft expands farther. The visible tornado becomes very wide, and eventually it will degenerate into a whole family of vortexes orbiting around a common center (see figure below). First two, then three, and so on. The little family may extend all the way to the cloud base, or may suddenly terminate in a double-celled vortex.
- Finally with increasing ambient swirl a very small amount of updraft leads to a situation where cyclostrophic balance occurs almost immediately. No concentrated vortex can possibly form. One might envisage this situation as one in which the mesocyclone itself descends to the ground as a huge dynamic pipe. Thus. below a thunderstrom in such a situation there is a huge circulation of air that is tens of kilometers in diameter. The winds may reach 100mph and the central pressure may be 30-40mb (3-4%) lower than in the surroundings.
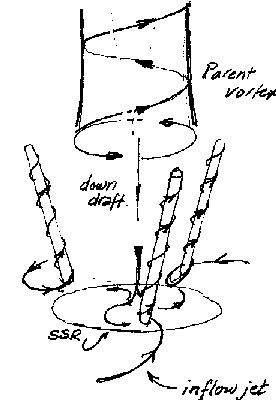
This drawing shows an intense parent vortex above with a downdraft in its core. The interaction of the downdraft with the ground surface increases the diameter of the vortex at its base, and causes it to degenerate into a family of three, smaller, but more intense vortexes, which T. Fujita once refered to as "suction spots." The family orbit around on a stagnant ring (SSR) where air diverging from the downdraft meets air drawn into the vortexes along the three jet inflows. The family of vortexes is usually compact, however, Ward suggested that the Newton, Kansas tornado of May 24, 1963, with its puzzling observations of multiple tornadoes moving in different directions, could be explained as a family of such multiple vortexes expanded out to a stagnant ring diameter of 1 mile.
Several images on this page are found at the web site of Wm. T. Hark. You can get more info and better resolution pictures there.
One topic back or one topic forward







