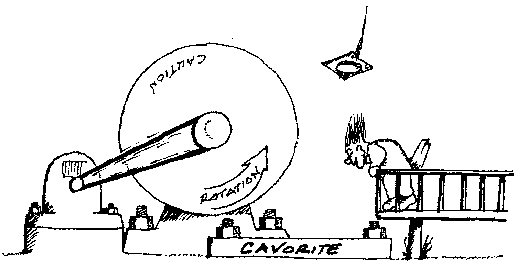
Figure 1. Our academic grips the guardrail to view the cavorite engine, but losses his mortar board. Notice the large bolts that are required to keep antigravity material attached to the earth.
Some years ago I put together a discussion of a few topics in perpetual motion and its relationship to thermodynamics. I'd produced this as a supplement for my engineering students, and subsequently edited it for the world wide web. It explored several topics in thermodynamics and perpetual motion not found anywhere else, as nearly as I knew. This past summer a professor emeritus, Dr. Donald E. Simanek, and I carried on a correspondence regarding some first law perpetual motions machines. Dr. Simanek's questions and discussion helped me form what I believe is an explanation about why a couple of mysterious first law machines cannot work.
The essense of Dr. Simanek's concerns is that using the first law of thermodynamics to explain why a first law meachine won't work is not persuasive to perpetual motion enthusiasts, and not very instructive to students either. He feels that a person ought to be able to show why a perpetual motion machine will not work from mechanical principles. This is a good point, and one I alluded to in my original work, but never explored. In particular, he asked, what is the mechanical flaw in my cartoon version of the Cavorite motor which will prevent it from working? I have included that cartoon for reference, below.

Figure 1. Our academic grips the guardrail to view the cavorite engine, but losses his mortar board. Notice the large bolts that are required to keep antigravity material attached to the earth.
He pointed out its similarity to another machine that has bothered him for a long time. I have produced a drawing of it below as well. This machine has an electrically charged rotor encased half inside a shielded slot. Below the rotor is an electrically charged plane. Allegedly the charged plane will repel the half of the rotor outside the slot, but have no effect on the half rotor inside the slot because the electrostatic shield negates the electrical field inside. The imbalanced electrical repulsion presumably will cause the rotor to turn. You can see the similarity to the Cavorite motor as I drew it.
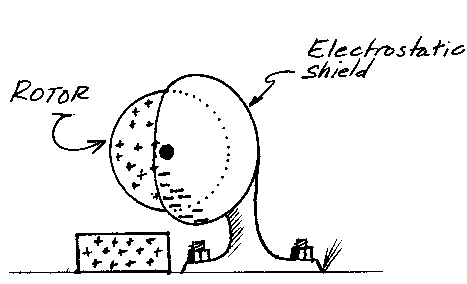
Figure 2. An electrostatic perpetual motion machine. Allegedly the rotor senses the charged plane only on the unshielded, left half, and this causes the rotor to accelerate. Notice how similar this specification is to the Cavorite motot of Figure 1. Thanks to Donald E. Simanek for this suggestion.
Dr. Simanek's argument is that either the Cavorite motor, or its electrostatic counterpart, do not actually change in any way as they rotate. Therefore, he reasons, by Stevin's principle of virtual work, no energy is gained during the rotation and either motor, once started, will eventually stop because of friction, or, if we neglect friction, neither motor provides useful output work.
Despite the utility of virtual work, it isn't always easy to apply the idea of virtual work to a rotating object. Jacob Den Hartog (Dover Ed. of Mechanics, p.?) summarizes Stevin's principle for a rotating body as supplying work if there is a force couple acting on a rotating body. It seems that deciding whether or not there is a force couple (torque) on the rotor is prerequisite to using Stevin's principle. Is there a force couple? It seems at first glance, that the antigravity properties of Cavorite provide just such a force couple.
In my discussions with Simanek, and in reading some references he provided, it appears that people who think about Cavorite (the are darned few who have) think of it as antigravity material or, if you wish, as negative mass. However, if Cavorite is nothing more than negative mass, Figure 3 shows why it will never produce a force couple.
Figure 3 shows a rotor charged uniformly positive. It is perfectly analogous to a rotor of uniform positive mass. There are two arbitrarily located point charges nearby, one positive and one negative (this one we can think of as a tiny bit of Cavorite). The negative source attracts each infinitesimal of charge in the wheel and the postive charge repels each one. If we integrate over the entire rotor, and resolve components of force, it turns out that there is a force to the right on the rotor, but there is no force couple around the axis. Likewise, each negative source of the gravity field in the Cavorite repels normal mass on one side of the wheel, but it also repels mass on the other side of the wheel. Presuming that Cavorite acts merely as negative mass may make it repel normal material, but will not make material circulate around an axle.
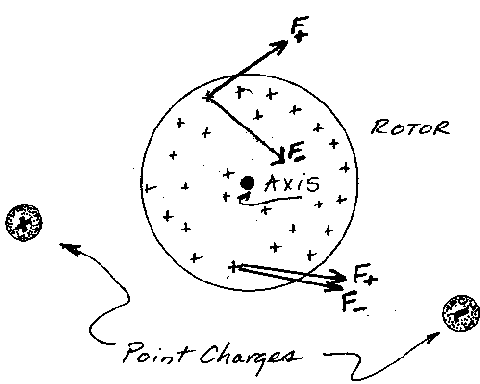
Figure 3. No matter how we arrange the point charges there may be a lateral force on the rotor axle, but never a force couple to turn the rotor. In this static situation the curl of E is always zero.
A person can see this also by reasoning that a force field having both positive and negative charges does not necessarily have a curl. If Cavorite were to exist, and allow the construction of a perpetual motion machine as I have drawn in my cartoon, then it would have to operate as follows. The Cavorite would have to alter the gravitational field in such a way that an element of the wheel would gain or loose gravitational potential energy as it made a path around the axle. Thus, Cavorite would produce a gravitational field no longer obtained from the gradient of a conservative potential field. In other words, Cavorite would have to produce a gravitational field with a curl.
Curl(g)<>0
Cavorite understood in this way would be the equivalent of a mass-current, and produce some gravitational equivalent to a magnetic field. Just as a magnetic monopole would circulate around a wire carrying electrical current, a mass particle would circulate around the axle of the Cavorite motor. Thus, my Cavorite cartoon motor ought to look like that in Figure 4, below. The professor's mortar board tries to fly an orbit around the axle, but gets centrifuged into the bushes to the left.
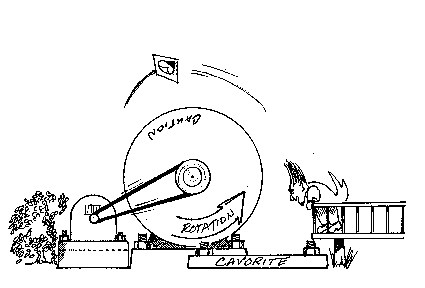
Figure 4. How the Cavorite motor would actually have to operate. Material would attempt to circulate around the axle of the motor, gaining kinetic energy with each orbit. Obviously the mortar board has nothing to keep it in orbit, so it ends its flight in the bushes.
In reality the gravitational field is conservative and has no curl, and wouldn't have a curl even if there were antigravity material. The electrical field, despite there being both positive and negative charges, is also conservative as long as there are no electrical currents and varying magnetic fields. The magnetic field itself is not necessarily conservative. The magnetic field can have a curl. For example, it has a curl at the center of a line current. If there were such a thing as a magnetic monopole, then one could be attached to a rotor hung on a current carrying axle, and the rotor would accelerate and even output work. Would this be a perpetual motion machine? It seems so, but that is a story for another time.
Finally, what about the charged rotor half in an electrostatic shield? Why won't it work. An electrostatic shield may provide a refuge from electrical fields inside, but it will also alter the external electrical field. In particular, negative charge will accumulate on the lower left of the shield as Figure 2 shows. Positive charge on the lower half of the rotor is attracted toward this negative charge and that attraction will negate any torque provided by repulsion from the slab of positive charge below. No matter how you may distribute positive charge outside the shield to provide torque, the induced charge on the shield will negate that torque.